Building Blocks for Deep Learning: Your First Custom Kernel with Triton

So, you’ve heard the buzz about OpenAI’s Triton and its ability to let you craft custom GPU kernels? Maybe you’re facing performance bottlenecks with standard deep learning operations, or perhaps you have a unique algorithm that existing libraries don’t quite cover. Whatever your reason, you’re in the right place! This winter break, I decided to dive into the fascinating world of high-performance GPU programming, and one of the most exciting tools I’ve discovered is Triton.

This blog post is your starting point on the journey of writing custom GPU kernels with Triton. We’ll begin with the very basics, crafting a simple kernel to illustrate the core concepts. Think of this as your “Hello, World!” for the world of high-performance GPU programming.

Why Triton? Taking Control of Your GPU

Before we dive into code, let’s briefly touch on why you might choose Triton. While libraries like PyTorch and TensorFlow provide highly optimized operations, there are scenarios where custom kernels offer advantages:

• Performance Optimization: For very specific operations, you can often achieve better performance by tailoring a kernel to the exact hardware and data layout.
• Implementing Novel Algorithms: If you’re working on cutting-edge research or specialized applications, you might need to implement algorithms not available in standard libraries.
• Fine-grained Control: Triton gives you a lower-level view of GPU execution, allowing for precise control over memory access and parallelism.

Triton makes this process surprisingly accessible. It provides a Python-like language that compiles down to efficient machine code for your GPU, bridging the gap between high-level abstraction and low-level control.

Your First Triton Kernel: Adding a Scalar

Let’s get our hands dirty with a simple example. We’ll write a Triton kernel that adds a scalar value to each element of an input tensor. Think of it this way: you have a collection of numbers (the tensor), and you want to increase each of those numbers by the same amount (the scalar). This is a fundamental operation, and while standard libraries can handle it, it’s a perfect starting point to understand how custom GPU kernels work.

What’s a Kernel, Anyway?

In the world of GPU programming, a “kernel” is essentially a function that’s designed to be executed across many processing cores on the GPU simultaneously. Imagine having thousands of tiny workers (threads), and you want them all to perform the same basic task on different pieces of data at the same time. That’s what a kernel allows you to do. In our case, we want each worker to add a scalar to a different number from our input tensor.

But how do we organize and manage these thousands of workers? That’s where the concepts of grids, blocks, and threads come in, as illustrated below:

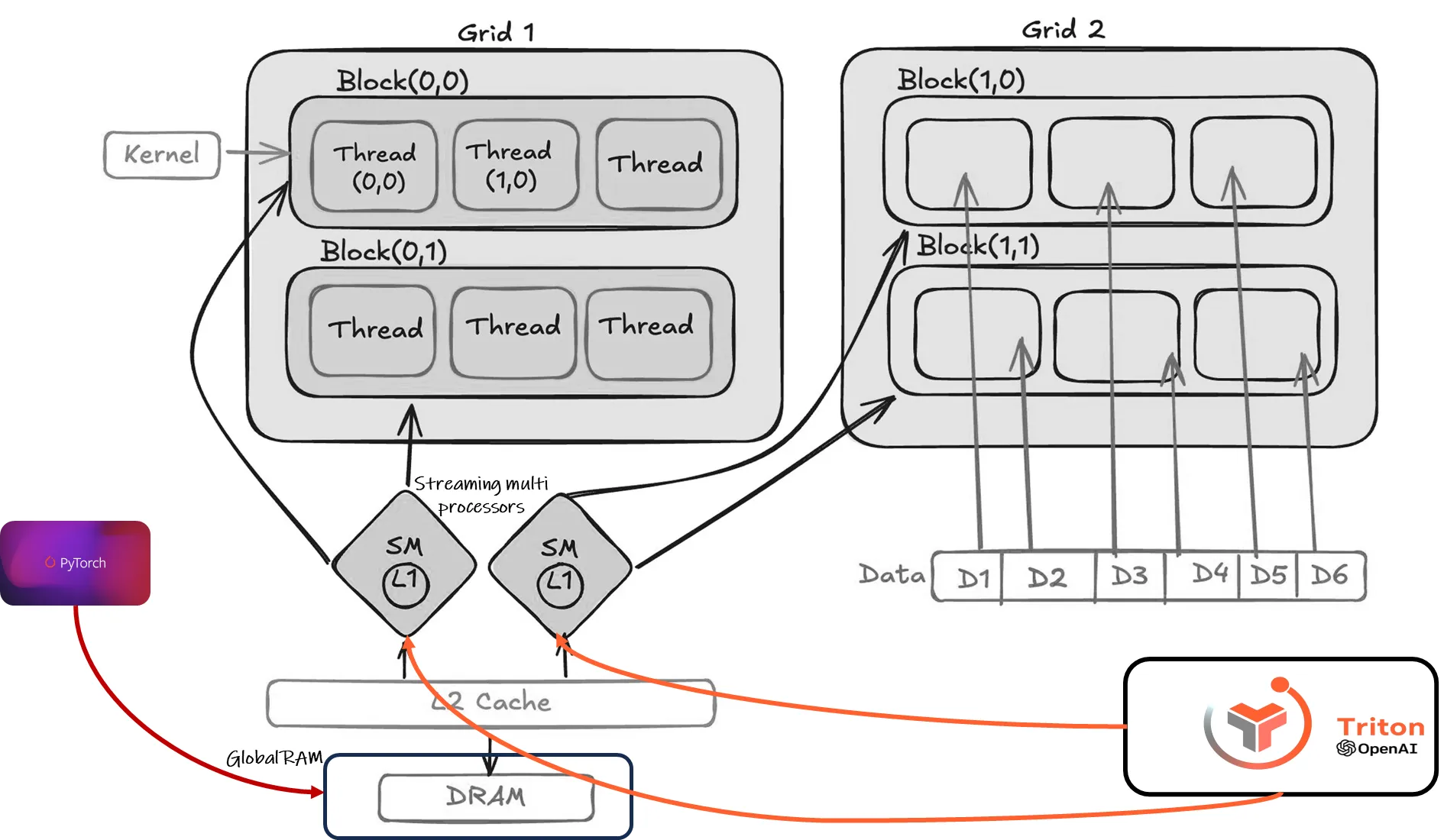
GPU Execution Model: Kernel, Grids, Blocks, and Threads. Credit: @Fellyralte

Let’s break down this diagram:

1. Kernel: The kernel is the function (like our add_scalar_kernel) that we want to run in parallel. You can see it represented by a gray box in the image pointing to the code that will run in each thread.

2. Thread: A thread is the basic unit of execution. Each thread executes the kernel code. In our diagram, each small box inside a block represents a thread, and each thread is responsible for processing one element (or a small chunk) of the input data. You can see them as white boxes inside the blocks, where the kernel code runs.

3. Block: A block is a group of threads. Blocks are crucial because threads within a block can cooperate and share data through fast on-chip shared memory (not shown in this simplified diagram). In the diagram, each grid is divided into blocks, like Block(0,0) and Block(1,0), which will run in parallel. Threads within a block are indexed using threadIdx.x, threadIdx.y, and threadIdx.z (for 3D blocks). You can see them in dark gray in the image, and how the indexing is made.

4. Grid: A grid is a collection of blocks. In the image, you see Grid 1 and Grid 2, which in this case is only one dimension, but could have more. When you launch a kernel, you specify the grid dimensions, essentially saying how many blocks you want in each dimension. You can see two grids in light gray in the image.

When it comes to these concepts, I really like this analogy: Think of a grid as an apartment building, a block as a floor in that building, and each apartment on that floor as a thread. Each apartment (thread) can work independently, but apartments on the same floor (block) can easily share resources like heat and water.

Execution Flow:

When we launch our add_scalar_kernel, here’s what happens conceptually:

1. Data Loading: Threads in a block cooperatively load data from global memory (DRAM) into the cache (and shared memory).

2. Computation: Each thread performs its computation (adding the scalar to its assigned element)

3. Data Writing: After computation, the threads write the results back to global memory (DRAM).

Why This Matters:

Understanding this execution model is essential for writing efficient GPU code. By carefully managing how we divide the work among grids, blocks, and threads and how we access memory, we can maximize parallelism and minimize latency, ultimately achieving significant speedups compared to running the same code on a CPU.

Let’s Go for Triton

Now that we understood the building blocks and concepts, we can start working on our add scalar kernel. In this kernel, each thread in each block will take one element from the input tensor, add the given scalar value to it, and then write the result to the corresponding position in the output tensor. Because we’ll launch many blocks (and therefore many threads) in parallel, each instance can work on a different element of the tensor independently. This is how we achieve massive speedups on the GPU.

Inputs and Outputs of Our Kernel

To perform its job, our kernel needs some information:

• The Input Tensor: This is the collection of numbers we want to modify.
• The Scalar Value: This is the single number that will be added to each element.
• A Place to Store the Results: The kernel needs to write the modified numbers back.
• Information about the Size: The kernel needs to know how many elements there are.
• How to Divide the Work: We need a way to tell each kernel instance which part of the tensor it should handle.

Pseudocode for Adding a Scalar

Before we see the actual Triton code, let’s express the logic of our kernel in pseudocode. This will help us understand the steps involved without getting caught up in the specific syntax of Triton:

Kernel: add_scalar_kernel(output_array, input_array, scalar, num_elements, block_size)

// Get the ID of this specific kernel instance
program_id = get_current_program_id()

// Calculate the starting index for this instance's block of work
block_start_index = program_id * block_size

// Calculate the indices of the elements this instance will process
element_indices = range(block_start_index, block_start_index + block_size)

// Loop through the elements this instance is responsible for
for index in element_indices:
// Make sure we don't go beyond the bounds of the input array
if index < num_elements:
// Load the input value at the current index
input_value = load_from_memory(input_array, index)

      // Add the scalar to the input value
      result = input_value + scalar

      // Store the result in the output array at the current index
      store_to_memory(output_array, index, result)

This pseudocode outlines the basic steps each instance of our kernel will perform. Notice how it focuses on the logic of accessing data, performing the addition, and storing the result, without delving into the specific Triton commands.

Your First Triton Kernel: The Code

Now, let’s see how this pseudocode translates into actual Triton code:

import torch
import triton
import triton.language as tl

@triton.jit
def add_scalar_kernel(
        output_ptr: tl.pointer_type,  # Explicit pointer type
        input_ptr: tl.pointer_type,  # Explicit pointer type
        scalar,  # float32 The scalar value to add - ensure it's a float!
        n_elements,  # int The number of elements in the tensor
        BLOCK_SIZE: tl.constexpr,
):
    """Kernel for adding a scalar to each element of a tensor."""
    pid = tl.program_id(axis=0)
    block_start = pid * BLOCK_SIZE
    offsets = block_start + tl.arange(0, BLOCK_SIZE)
    mask = offsets < n_elements
    x = tl.load(input_ptr + offsets, mask=mask)
    output = x + scalar
    tl.store(output_ptr + offsets, output, mask=mask)

Let’s break down the key components:

@triton.jit: This decorator is crucial. It tells Triton to just-in-time compile this Python function into an optimized GPU kernel.

Kernel Function Definition:

add_scalar_kernel(...): This defines our kernel function. Notice the arguments: pointers to tensors (output_ptr, input_ptr), the scalar value, and the number of elements. Working with raw memory pointers is common in GPU programming for efficiency.

BLOCK_SIZE: tl.constexpr: This declares BLOCK_SIZE as a compile-time constant. Triton uses this information to optimize the generated code. We’ll see how to set this later. Note: Choosing the right block size is important for performance. It’s often related to the hardware’s warp size (typically 32 for NVIDIA GPUs), and powers of 2 are generally preferred.

pid = tl.program_id(axis=0): This is where the parallelism starts. When you launch a Triton kernel, you launch many independent “program instances” (think of them as lightweight threads). tl.program_id(axis=0) gives each instance a unique ID along the specified axis (in this case, the 0th axis). This allows different parts of the tensor to be processed concurrently.

block_start = pid * BLOCK_SIZE: We divide the tensor into blocks of size BLOCK_SIZE. Each program instance is responsible for processing one block. This line calculates the starting index for the current block.

offsets = block_start + tl.arange(0, BLOCK_SIZE): This creates a range of indices within the current block. tl.arange is similar to torch.arange but operates within the Triton language.

mask = offsets < n_elements: This is important for handling boundary conditions. If the total number of elements isn’t perfectly divisible by BLOCK_SIZE, some program instances might have offsets that go beyond the tensor’s bounds. The mask ensures we only operate on valid indices.

x = tl.load(input_ptr + offsets, mask=mask): This line loads a block of data from the input tensor into a register. input_ptr + offsets calculates the memory address to load from. The mask ensures we only load valid elements.

output = x + scalar: This performs the core operation: adding the scalar to the loaded block of data.

tl.store(output_ptr + offsets, output, mask=mask): This writes the result back to the output tensor in GPU memory, again using the mask for safety.

Running Your Triton Kernel

Now that we’ve defined our kernel, let’s see how to execute it:

def add_scalar(output, input, scalar):
    n_elements = output.numel()
    BLOCK_SIZE = 1024 # A good starting point for block size
    grid = (triton.cdiv(n_elements, BLOCK_SIZE),)

    # Ensure scalar is a float (or cast if necessary)
    scalar = float(scalar)

    add_scalar_kernel[grid](
        output_ptr=output,  # Pass pointer to data
        input_ptr=input,  # Pass pointer to data
        scalar=scalar,
        n_elements=n_elements,
        BLOCK_SIZE=BLOCK_SIZE,
    )

# Example usage (using a size divisible by BLOCK_SIZE but its not necessary):
input_tensor = torch.rand(1024 * 5, device='cuda')
output_tensor = torch.empty_like(input_tensor)
scalar_value = 5.0

add_scalar(output_tensor, input_tensor, scalar_value)

# Verify the result
torch.testing.assert_close(output_tensor, input_tensor + scalar_value)
print("Triton kernel executed successfully!")

Here’s what’s happening in the Python code:

add_scalar(output, input, scalar): This is a Python function that wraps the Triton kernel call, making it easier to use.

n_elements = output.numel(): We get the total number of elements in the tensor.

BLOCK_SIZE = 1024: We define the block size.

grid = (triton.cdiv(n_elements, BLOCK_SIZE),): This defines the grid of program instances. We need enough instances to cover all elements of the tensor. triton.cdiv (ceiling division) ensures we have enough blocks even if n_elements is not perfectly divisible by BLOCK_SIZE. The ( ... ,) creates a tuple, as the grid can have multiple dimensions for more complex kernels.

add_scalar_kernel[grid](...): This is how we launch the Triton kernel. The [grid] notation specifies the number of program instances to launch. We then pass the arguments to the kernel, mapping the Python variables to the kernel’s parameters.

A Slightly More Complex Example: Element-wise Multiplication

To solidify your understanding, let’s look at another simple kernel – element-wise multiplication of two tensors:

@triton.jit
def multiply_tensors_kernel(
        output_ptr ,
        input1_ptr ,
        input2_ptr,
        n_elements,
        BLOCK_SIZE: tl.constexpr,
):
    pid = tl.program_id(axis=0)
    block_start = pid * BLOCK_SIZE
    offsets = block_start + tl.arange(0, BLOCK_SIZE)
    mask = offsets < n_elements
    x1 = tl.load(input1_ptr + offsets, mask=mask)
    x2 = tl.load(input2_ptr + offsets, mask=mask)
    output = x1 * x2
    tl.store(output_ptr + offsets, output, mask=mask)

def multiply_tensors(output, input1, input2):
    n_elements = output.numel()
    BLOCK_SIZE = 1024
    grid = (triton.cdiv(n_elements, BLOCK_SIZE),)
    multiply_tensors_kernel[grid](
        output_ptr=output,
        input1_ptr=input1,
        input2_ptr=input2,
        n_elements=n_elements,
        BLOCK_SIZE=BLOCK_SIZE,
    )

# Example usage:
tensor_a = torch.rand(1024 * 5, device='cuda', dtype=torch.float32)
tensor_b = torch.rand(1024 * 5, device='cuda', dtype=torch.float32)
output_mult = torch.empty_like(tensor_a)

multiply_tensors(output_mult, tensor_a, tensor_b)
torch.testing.assert_close(output_mult, tensor_a * tensor_b)
print("Element-wise multiplication kernel executed successfully!")

This kernel is very similar to the scalar addition example. The main difference is that we now load data from two input tensors (input1_ptr and input2_ptr) and perform element-wise multiplication.

Triton vs PyTorch Performance

To see how our Triton kernels perform, we benchmarked them against PyTorch’s built-in functions. This involved measuring the execution time of both for operations like scalar addition and element-wise multiplication across various tensor sizes. We ran each test multiple times to ensure accuracy and warmed up the GPU beforehand. The detailed benchmarking code and performance plots are available in the GitHub repository. When we run benchmarks, we can see the performance advantage of using Triton.

As we’ve seen from the benchmarks, while PyTorch offers excellent performance for smaller operations, Triton’s ability to leverage the GPU’s parallel processing capabilities truly shines when we move to larger tensor sizes. The crossover point, where Triton surpasses PyTorch in performance, is particularly noteworthy. In the realm of deep learning, where large matrix operations are commonplace, this is precisely where custom kernels can provide a significant edge.

Note: Hyper-parameters such as BLOCK_SIZE are shown to be effective in the performance results. For this example, we assumed (with some preliminary test :) ) that the process is IO bounded and number of blocks wouldn’t effect the performance.

Conclusion: Your Triton Journey Begins

Congratulations! You’ve written and executed your first custom Triton kernels. You’ve learned about the basic structure of a Triton kernel, how to launch it, and how to handle memory access and parallelism.

This is just the beginning. In the next blog post, we will delve into matrix multiplication, a cornerstone of neural networks, and see how Triton’s strengths can be further exploited to achieve remarkable performance gains.